polígonos
esta entrada va dedicada a riesgho, por ser quien me dio la idea. además sé que a ella le gustan estas cosas. :)
voy a contaros lo mejor que sepa cómo se construyen gráficamente algunos polígonos regulares. se entiende por ‘gráficamente’, empleando tan sólo lápiz, regla, escuadra/cartabón y compás. la regla se utilizará para trazar líneas rectas, no se realizará ninguna medición con ella. asimismo, tampoco se utilizará medidor de ángulos, no será necesario.
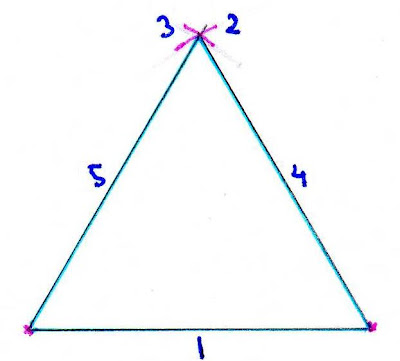
empezaremos por el polígono regular más sencillo, que es el triángulo equilátero. es también el más fácil de dibujar.
los pasos a seguir son los siguientes: trazamos con la regla una línea recta horizontal (aunque en realidad podría tener cualquier dirección, pero lo hacemos así para que se vea más claro) de la longitud que queramos: [1]. a continuación abrimos el compás con un radio igual a esa longitud que hemos trazado.
pinchamos con el compás en cada uno de los extremos de la línea base, y trazamos sendos arcos que se corten en un punto: [2] y [3]. unimos los extremos de la línea con ese punto de corte, y sin darnos cuenta ya tenemos trazados los tres lados del triángulo: [4] y [5].
el siguiente polígono regular que analizaremos es el cuadrado. también es muy sencillo de dibujar, y dada su regularidad y simetría, existen muchos métodos alternativos para hacerlo.
una manera de dibujarlo es la siguiente: trazamos una línea recta de la longitud que queramos, que será la base: [1]. desde uno cualquiera de los extremos de esta línea, trazamos una perpendicular con ayuda de la escuadra y el cartabón: [2].
abrimos el compás con un radio igual a la longitud que le hemos dado al lado base. pinchamos el compás en el punto desde donde acabamos de trazar la línea perpendicular a la base, y trazamos un arco que corte a dicha perpendicular: [3]. y atención, desde el punto de corte de ese pequeño arco con la perpendicular, ahora trazamos una paralela a la base: [4].
ahora tenemos varias alternativas para terminar de dibujar el cuadrado. la que seguiremos será trazar otra línea perpendicular a la base desde el otro extremo de ésta: [5]. de ese modo el cuadrado queda cerrado automáticamente, y ya no hemos tenido que repetir el paso de llevar con el compás la longitud del lado ni nada de eso...
voy a contaros lo mejor que sepa cómo se construyen gráficamente algunos polígonos regulares. se entiende por ‘gráficamente’, empleando tan sólo lápiz, regla, escuadra/cartabón y compás. la regla se utilizará para trazar líneas rectas, no se realizará ninguna medición con ella. asimismo, tampoco se utilizará medidor de ángulos, no será necesario.
empezaremos por el polígono regular más sencillo, que es el triángulo equilátero. es también el más fácil de dibujar.
los pasos a seguir son los siguientes: trazamos con la regla una línea recta horizontal (aunque en realidad podría tener cualquier dirección, pero lo hacemos así para que se vea más claro) de la longitud que queramos: [1]. a continuación abrimos el compás con un radio igual a esa longitud que hemos trazado.
pinchamos con el compás en cada uno de los extremos de la línea base, y trazamos sendos arcos que se corten en un punto: [2] y [3]. unimos los extremos de la línea con ese punto de corte, y sin darnos cuenta ya tenemos trazados los tres lados del triángulo: [4] y [5].

el siguiente polígono regular que analizaremos es el cuadrado. también es muy sencillo de dibujar, y dada su regularidad y simetría, existen muchos métodos alternativos para hacerlo.
una manera de dibujarlo es la siguiente: trazamos una línea recta de la longitud que queramos, que será la base: [1]. desde uno cualquiera de los extremos de esta línea, trazamos una perpendicular con ayuda de la escuadra y el cartabón: [2].
abrimos el compás con un radio igual a la longitud que le hemos dado al lado base. pinchamos el compás en el punto desde donde acabamos de trazar la línea perpendicular a la base, y trazamos un arco que corte a dicha perpendicular: [3]. y atención, desde el punto de corte de ese pequeño arco con la perpendicular, ahora trazamos una paralela a la base: [4].
ahora tenemos varias alternativas para terminar de dibujar el cuadrado. la que seguiremos será trazar otra línea perpendicular a la base desde el otro extremo de ésta: [5]. de ese modo el cuadrado queda cerrado automáticamente, y ya no hemos tenido que repetir el paso de llevar con el compás la longitud del lado ni nada de eso...
el pentágono regular es complicado de dibujar, mientras que el hexágono regular es relativamente sencillo. por eso empezaremos por el hexágono, y el pentágono lo dejaremos para el final.
esta vez el primer paso no será trazar una línea recta. lo primero que haremos será trazar una circunferencia del radio que deseemos: [1]. si queremos la podemos hacer en trazo tenue, al ser una figura auxiliar que no debe eclipsar a la estrella, que será el hexágono. ;)
mantenemos el compás abierto con ese radio. pinchamos en un punto cualquiera de la circunferencia (del perímetro exterior), y trazamos un pequeño arco que corte a la propia circunferencia: [2].
pinchamos con el compás en el punto de corte de ese arco con la circunferencia, y trazamos un nuevo arco que corte a ésta: [3]. repetimos el proceso: [4], [5] y [6].
este método se basa en la propiedad de que el lado de un hexágono regular inscrito en una circunferencia es igual al radio de dicha circunferencia. si desde [6] pinchamos y trazamos otro arco, cortará sobre el punto donde hemos pinchado por primera vez. se veía venir...
y por último, unimos los puntos de corte de los pequeños arcos con la circunferencia base que hemos trazado al principio, y ya tenemos dibujado el hexágono. como este último paso es igual en todos los casos y lo más difícil ya está hecho, he empleado sólo un número para denotarlo: [7].

vamos, por fin, con el pentágono, que como digo es complicado. hay que explicar algunos conceptos preliminares antes de abordar su construcción gráfica.
la propiedad del pentágono en la que nos vamos a apoyar es la siguiente: la proporción entre la longitud de una ‘diagonal’ cualquiera -es decir, una línea que una dos vértices no consecutivos cualesquiera- y la longitud del lado del pentágono es igual al número áureo. es decir, la longitud de una ‘diagonal’ del pentágono es la longitud del lado multiplicada por el número áureo.
el valor del número áureo es (1+√5)/2. este valor se deduce de la propia definición de la proporción áurea, y de eso hablaré más detenidamente en una futura entrada. ;) lo que nos interesa en este caso es que ese número, cuyo valor se puede aproximar tanto como se quiera según dónde se trunque la serie infinita de decimales que tiene (1.61803398875...), lo podemos representar gráficamente.
(1+√5)/2 es lo mismo que 1/2+√5/2. la proporción 1/2 es muy sencilla de obtener gráficamente: dada una longitud, obtenemos su mitad, trazando la mediatriz, por ejemplo. en cuanto a la proporción √5/2, será la mitad de la proporción √5. y cómo obtenemos la proporción √5? cuál es su equivalente geométrico? vamos a verlo.
dado un triángulo rectángulo con catetos de longitudes 1 y 2 unidades, por el teorema de pitágoras, la longitud de la hipotenusa será √5. en general, para cualquier triángulo rectángulo en el que los catetos estén en proporción 1:2, la longitud de la hipotenusa será √5 por la longitud del cateto menor.

por tanto, para un triángulo rectángulo cuyos catetos midan, esta vez, 1/2 y 1 unidades de longitud, la hipotenusa irá reducida en la misma proporción: medirá √5/2. con esto nos vamos a quedar para la construcción del pentágono.
lo primero que haremos será trazar una línea horizontal de una amplitud considerable, pues sobre ella tendremos que hacer diversas construcciones auxiliares. sobre parte de esa línea marcamos en un trazo más grueso el lado base del pentágono, con la longitud que queramos: [1].
abrimos el compás con un radio igual a la longitud del lado. desde un extremo de éste trazamos un arco que corte a la larga línea recta que hemos trazado para posteriores construcciones: [2]. de algún modo, hemos trazado un nuevo segmento de longitud igual al lado base. lo que haremos ahora con ese segmento será “partirlo por la mitad”. cómo? trazando su mediatriz.
nos situamos en los extremos de esa línea. desde cada uno de ellos trazamos dos arcos de cualquier radio (eso ahora mismo no importa) con tal de que se corten por encima de la línea: [3]. algo parecido a lo que hacíamos para dibujar el triángulo. ahora volvemos a hacer lo mismo: trazamos desde los extremos de la línea dos arcos que se corten, pero esta vez se cortarán por debajo: [4]. unimos los puntos de corte que hemos obtenido en [3] y [4] y nos sale una recta perpendicular que corta por la mitad a la línea en cuestión.
desde el extremo exterior de esa línea que acabamos de partir por la mitad, trazamos una perpendicular con la escuadra y el cartabón: [5]. abrimos el compás con un radio igual al lado base del pentágono, pinchamos en ese extremo desde el que hemos trazado la línea perpendicular, y trazamos un arco que corte a la misma: [6]. os recordará a lo que hicimos para el cuadrado.
ahora podemos unir ese último punto de corte obtenido en [6] con el punto medio resultante de dividir en dos mitades iguales la línea auxiliar de longitud igual al lado del pentágono. los unimos y obtenemos una línea diagonal: [7]. este paso no es estrictamente necesario, pero sirve para comprender lo que estamos haciendo.
hemos obtenido un triángulo rectángulo cuyos catetos miden -tomando el lado del pentágono como unidad de referencia sobre la cual establecemos las proporciones- 1/2 y 1 unidades (el horizontal y el vertical, respectivamente). cuánto medirá entonces la hipotenusa, que es la línea que hemos trazado en [7]? por lo que hemos explicado unos párrafos más arriba, medirá √5/2.
atención a lo que hacemos ahora: pinchamos el compás en el punto de corte de la mediatriz con la línea auxiliar, y lo abrimos con un radio igual a la última diagonal que hemos trazado. dicho de otro modo, lo abrimos hasta el extremo de esa diagonal. a partir de ahí, trazamos un arco con ese radio que vaya bajando hasta que corte a la larga línea horizontal que trazamos al principio de todo: [8].
la distancia que hay desde el extremo del lado base hasta el punto de corte de la mediatriz con la línea auxiliar es 1/2 -considerando que el lado del pentágono mide 1 unidad-. y la distancia que va desde el punto de corte de la mediatriz hasta el punto de corte del arco que acabamos de trazar y que hemos obtenido en [8] es √5/2. lo que hemos hecho es poner las dos distancias seguidas sobre una misma línea recta, de tal manera que se puedan sumar. así, hemos obtenido gráficamente el valor 1/2+√5/2, o lo que es lo mismo, (1+√5)/2: la proporción áurea.
lo más difícil ya está hecho, lo que queda es mecánico. abrimos el compás con un radio que va desde el extremo del lado base hasta el último punto de corte, obtenido en [8]. este radio no es otro que el número áureo, o para decirlo con mayor propiedad, la longitud del lado del pentágono multiplicada por el número áureo.
desde los extremos del lado base del pentágono trazamos dos arcos con ese ‘radio áureo’ que se corten en un punto: [9] y [10]. aunque no es necesario, podemos unir ese punto de corte con los extremos del lado base: [11] y [12]. es un triángulo isósceles cuya base es el lado del pentágono y cuyos lados laterales son las ‘diagonales’. es como el ‘armazón interno’ del pentágono, y verlo dibujado sirve para entender mejor lo que estamos haciendo.
abrimos el compás ahora con un radio igual a la longitud del lado del pentágono. desde los dos extremos de una de las diagonales, por ejemplo la obtenida en [11], trazamos dos arcos que se corten en un punto: [13] y [14]. unimos ese punto de corte con los extremos de la diagonal, y ya tenemos dos lados más del pentágono: [15] y [16].
ahora hacemos lo mismo, pero al otro lado: desde los extremos de la diagonal obtenida en [12], y con radio igual al lado del pentágono, trazamos dos arcos que se corten en un punto: [17] y [18]. ese punto de corte lo unimos con los extremos de la diagonal, y... voilà! ya tenemos los dos lados que nos faltaban, y el pentágono cerrado por fin: [19] y [20].

creía que nunca acabaría de explicarlo! :D hice los dibujos de esta entrada y los escaneé hace bastantes días. sabía que el pentágono era la más complicada de las figuras, pero no hasta el punto de que me haya ocupado más espacio que el triángulo, el cuadrado y el hexágono juntos!
sé de alguna de vosotras que hace manualidades y bordados de forma pentagonal... ;) no os parece terrible?? el pentágono es complicadísimo, es una pesadilla!! :D
esta vez el primer paso no será trazar una línea recta. lo primero que haremos será trazar una circunferencia del radio que deseemos: [1]. si queremos la podemos hacer en trazo tenue, al ser una figura auxiliar que no debe eclipsar a la estrella, que será el hexágono. ;)
mantenemos el compás abierto con ese radio. pinchamos en un punto cualquiera de la circunferencia (del perímetro exterior), y trazamos un pequeño arco que corte a la propia circunferencia: [2].
pinchamos con el compás en el punto de corte de ese arco con la circunferencia, y trazamos un nuevo arco que corte a ésta: [3]. repetimos el proceso: [4], [5] y [6].
este método se basa en la propiedad de que el lado de un hexágono regular inscrito en una circunferencia es igual al radio de dicha circunferencia. si desde [6] pinchamos y trazamos otro arco, cortará sobre el punto donde hemos pinchado por primera vez. se veía venir...
y por último, unimos los puntos de corte de los pequeños arcos con la circunferencia base que hemos trazado al principio, y ya tenemos dibujado el hexágono. como este último paso es igual en todos los casos y lo más difícil ya está hecho, he empleado sólo un número para denotarlo: [7].

vamos, por fin, con el pentágono, que como digo es complicado. hay que explicar algunos conceptos preliminares antes de abordar su construcción gráfica.
la propiedad del pentágono en la que nos vamos a apoyar es la siguiente: la proporción entre la longitud de una ‘diagonal’ cualquiera -es decir, una línea que una dos vértices no consecutivos cualesquiera- y la longitud del lado del pentágono es igual al número áureo. es decir, la longitud de una ‘diagonal’ del pentágono es la longitud del lado multiplicada por el número áureo.
el valor del número áureo es (1+√5)/2. este valor se deduce de la propia definición de la proporción áurea, y de eso hablaré más detenidamente en una futura entrada. ;) lo que nos interesa en este caso es que ese número, cuyo valor se puede aproximar tanto como se quiera según dónde se trunque la serie infinita de decimales que tiene (1.61803398875...), lo podemos representar gráficamente.
(1+√5)/2 es lo mismo que 1/2+√5/2. la proporción 1/2 es muy sencilla de obtener gráficamente: dada una longitud, obtenemos su mitad, trazando la mediatriz, por ejemplo. en cuanto a la proporción √5/2, será la mitad de la proporción √5. y cómo obtenemos la proporción √5? cuál es su equivalente geométrico? vamos a verlo.
dado un triángulo rectángulo con catetos de longitudes 1 y 2 unidades, por el teorema de pitágoras, la longitud de la hipotenusa será √5. en general, para cualquier triángulo rectángulo en el que los catetos estén en proporción 1:2, la longitud de la hipotenusa será √5 por la longitud del cateto menor.

por tanto, para un triángulo rectángulo cuyos catetos midan, esta vez, 1/2 y 1 unidades de longitud, la hipotenusa irá reducida en la misma proporción: medirá √5/2. con esto nos vamos a quedar para la construcción del pentágono.
lo primero que haremos será trazar una línea horizontal de una amplitud considerable, pues sobre ella tendremos que hacer diversas construcciones auxiliares. sobre parte de esa línea marcamos en un trazo más grueso el lado base del pentágono, con la longitud que queramos: [1].
abrimos el compás con un radio igual a la longitud del lado. desde un extremo de éste trazamos un arco que corte a la larga línea recta que hemos trazado para posteriores construcciones: [2]. de algún modo, hemos trazado un nuevo segmento de longitud igual al lado base. lo que haremos ahora con ese segmento será “partirlo por la mitad”. cómo? trazando su mediatriz.
nos situamos en los extremos de esa línea. desde cada uno de ellos trazamos dos arcos de cualquier radio (eso ahora mismo no importa) con tal de que se corten por encima de la línea: [3]. algo parecido a lo que hacíamos para dibujar el triángulo. ahora volvemos a hacer lo mismo: trazamos desde los extremos de la línea dos arcos que se corten, pero esta vez se cortarán por debajo: [4]. unimos los puntos de corte que hemos obtenido en [3] y [4] y nos sale una recta perpendicular que corta por la mitad a la línea en cuestión.
desde el extremo exterior de esa línea que acabamos de partir por la mitad, trazamos una perpendicular con la escuadra y el cartabón: [5]. abrimos el compás con un radio igual al lado base del pentágono, pinchamos en ese extremo desde el que hemos trazado la línea perpendicular, y trazamos un arco que corte a la misma: [6]. os recordará a lo que hicimos para el cuadrado.
ahora podemos unir ese último punto de corte obtenido en [6] con el punto medio resultante de dividir en dos mitades iguales la línea auxiliar de longitud igual al lado del pentágono. los unimos y obtenemos una línea diagonal: [7]. este paso no es estrictamente necesario, pero sirve para comprender lo que estamos haciendo.
hemos obtenido un triángulo rectángulo cuyos catetos miden -tomando el lado del pentágono como unidad de referencia sobre la cual establecemos las proporciones- 1/2 y 1 unidades (el horizontal y el vertical, respectivamente). cuánto medirá entonces la hipotenusa, que es la línea que hemos trazado en [7]? por lo que hemos explicado unos párrafos más arriba, medirá √5/2.
atención a lo que hacemos ahora: pinchamos el compás en el punto de corte de la mediatriz con la línea auxiliar, y lo abrimos con un radio igual a la última diagonal que hemos trazado. dicho de otro modo, lo abrimos hasta el extremo de esa diagonal. a partir de ahí, trazamos un arco con ese radio que vaya bajando hasta que corte a la larga línea horizontal que trazamos al principio de todo: [8].
la distancia que hay desde el extremo del lado base hasta el punto de corte de la mediatriz con la línea auxiliar es 1/2 -considerando que el lado del pentágono mide 1 unidad-. y la distancia que va desde el punto de corte de la mediatriz hasta el punto de corte del arco que acabamos de trazar y que hemos obtenido en [8] es √5/2. lo que hemos hecho es poner las dos distancias seguidas sobre una misma línea recta, de tal manera que se puedan sumar. así, hemos obtenido gráficamente el valor 1/2+√5/2, o lo que es lo mismo, (1+√5)/2: la proporción áurea.
lo más difícil ya está hecho, lo que queda es mecánico. abrimos el compás con un radio que va desde el extremo del lado base hasta el último punto de corte, obtenido en [8]. este radio no es otro que el número áureo, o para decirlo con mayor propiedad, la longitud del lado del pentágono multiplicada por el número áureo.
desde los extremos del lado base del pentágono trazamos dos arcos con ese ‘radio áureo’ que se corten en un punto: [9] y [10]. aunque no es necesario, podemos unir ese punto de corte con los extremos del lado base: [11] y [12]. es un triángulo isósceles cuya base es el lado del pentágono y cuyos lados laterales son las ‘diagonales’. es como el ‘armazón interno’ del pentágono, y verlo dibujado sirve para entender mejor lo que estamos haciendo.
abrimos el compás ahora con un radio igual a la longitud del lado del pentágono. desde los dos extremos de una de las diagonales, por ejemplo la obtenida en [11], trazamos dos arcos que se corten en un punto: [13] y [14]. unimos ese punto de corte con los extremos de la diagonal, y ya tenemos dos lados más del pentágono: [15] y [16].
ahora hacemos lo mismo, pero al otro lado: desde los extremos de la diagonal obtenida en [12], y con radio igual al lado del pentágono, trazamos dos arcos que se corten en un punto: [17] y [18]. ese punto de corte lo unimos con los extremos de la diagonal, y... voilà! ya tenemos los dos lados que nos faltaban, y el pentágono cerrado por fin: [19] y [20].

creía que nunca acabaría de explicarlo! :D hice los dibujos de esta entrada y los escaneé hace bastantes días. sabía que el pentágono era la más complicada de las figuras, pero no hasta el punto de que me haya ocupado más espacio que el triángulo, el cuadrado y el hexágono juntos!
sé de alguna de vosotras que hace manualidades y bordados de forma pentagonal... ;) no os parece terrible?? el pentágono es complicadísimo, es una pesadilla!! :D

Comentarios
Publicar un comentario