baldosas
cuando veo las baldosas de la calle o del interior de algún edificio, a menudo me fijo en el dibujo geométrico que forman, y me pongo a pensar cómo se podría reproducir sobre una lámina, con los instrumentos de dibujo habituales: lápiz, compás, regla, escuadra y cartabón.
sabía que antes o después escribiría alguna entrada sobre baldosas, pero hay muchas que tienen dibujos interesantes y nunca sabía cuál elegir como ejemplo. hace poco he sabido que las baldosas de bilbao -ciudad que he visitado en numerosas ocasiones desde mi infancia debido a los vínculos familiares que me unen a ella- son únicas y tienen mucha historia. por eso he decidido rendir un homenaje a la baldosa de bilbao. ;)
lo primero de todo es dibujar un cuadrado, de la longitud del lado que se desee, pero a ser posible amplio para poder hacer construcciones sobre él cómodamente: [1]. en aquella entrada que escribí sobre los polígonos, tenéis explicado cómo dibujar un cuadrado. ;)
a continuación vamos a dividir sus lados en tres partes iguales en horizontal y en vertical, para obtener 3x3 cuadrados cuyo lado sería un tercio del lado del original.
empezaremos dividiendo el lado vertical izquierdo en tres partes iguales. para ello utilizaremos el teorema de thales. nos serviremos de las propias líneas del cuadrado, con objeto de no trazar líneas adicionales que compliquen más el dibujo. sobre el lado horizontal inferior del cuadrado, llevamos una misma distancia, elegida a voluntad, tres veces: [2]. trazamos una línea que una el extremo más ‘lejano’, donde hemos llevado esa distancia por tercera vez, con el vértice superior izquierdo del cuadrado; desde el punto del lado horizontal donde nos hemos llevado la distancia arbitraria por segunda vez, trazamos una paralela a la última línea citada; y desde el punto donde nos hemos llevado por primera vez la distancia ‘de thales’, trazamos otra paralela a esa línea; de ese modo, hemos dividido el lado vertical izquierdo en tres partes iguales: [3].
desde los puntos que marcan la división de ese lado, trazamos sendas líneas paralelas al lado horizontal del cuadrado: [4]. de ese modo, hemos dividido el cuadrado en tres ‘rebanadas’ o capas horizontales del mismo espesor.
a continuación haremos algo análogo desde el lado horizontal, y por seguir un orden, lo haremos en el superior. para dividirlo en tres partes iguales no será necesario aplicar el teorema de thales nuevamente. como ya tenemos dividido el lado vertical, tomamos con el compás la longitud de ‘un tercio de lado’, y desde el vértice del cuadrado la llevamos dos veces sucesivamente: [5]. desde esos puntos que dividen el lado horizontal en tres partes iguales, trazamos dos paralelas al lado vertical del cuadrado: [6]. como ya estaba cortado en tres ‘rebanadas’ horizontales, al darle esos nuevos cortes verticales, lo hemos convertido en 9 cuadrados de 1/3 de lado del original, en disposición 3x3.
ahora viene la parte quizá más delicada. antes que nada, vamos a trazar las dos diagonales del cuadrado grande, el original, pues nos van a hacer falta: [7] y [8]. las hacemos en trazo fino para no perjudicar mucho la estética del dibujo.
con centro en el punto de corte de las dos diagonales, que es el centro del cuadrado grande, trazaremos una circunferencia cuyo radio será la mitad del lado del cuadrado pequeño. será una circunferencia inscrita en dicho cuadrado. para ello, desde el punto de corte de las diagonales trazaremos una paralela al lado vertical del cuadrado. donde corte al lado horizontal del cuadrado pequeño, será por donde deba pasar: [9]. así pues, trazamos la circunferencia, que deberá ser tangente a los lados del cuadrado: [10]. la construcción nunca será exacta, y para que se parezca a como son estas baldosas en la realidad, es mejor que la circunferencia se pase un poco de grande, que se salga ligeramente de los límites del cuadrado.
lo que viene ahora es más fácil de entender intuitivamente que de explicar. el dibujo de la baldosa de bilbao es similar a una flor con cuatro pétalos. y aunque estos pétalos están próximos, no llegan a tocarse entre sí. los cuatro pétalos son arcos de circunferencia que pasan por los puntos medios de los lados de los cuatro cuadrados pequeños que se encuentran en las esquinas del cuadrado grande. esto podría hacer pensar que su radio es igual a la mitad del lado del cuadrado pequeño, al igual que la circunferencia central. pero no es así, en realidad es un poco más pequeño. en consecuencia, el centro de la circunferencia del ‘pétalo’ no está exactamente en el vértice del cuadrado pequeño, sino ligeramente más adentro, aunque eso sí, en su diagonal.
dado que no he logrado encontrar las medidas o proporciones exactas de las baldosas de bilbao, lo haremos de forma aproximada. aunque, eso sí, siendo coherentes y manteniendo las medidas que hayamos elegido en un principio. nos situamos en el cuadrado pequeño de la esquina superior izquierda. trazamos la mediatriz del lado inferior de este cuadrado para hallar su punto medio: [11]. en la entrada de los polígonos también explicaba cómo trazar una mediatriz, lo digo por no alargar más esto, que parece la biblia. :D bien, nos fijamos en dónde la mediatriz ha cortado a la diagonal, y desde ese punto de corte trazamos una paralela al lado horizontal del cuadrado. de ese modo dividimos también en dos el lado vertical del cuadrado sin tener que trazar una nueva mediatriz: [12].
elegimos un punto próximo al vértice del cuadrado pequeño, que se encuentre en el interior del mismo y en su diagonal. desde ese punto comenzamos a trazar una circunferencia que pase por los puntos medios de los lados del cuadrado que acabamos de determinar, y detenemos su trazado cuando corte a la circunferencia central: [13].
a continuación haremos lo mismo en el cuadrado pequeño superior derecho, pero esta vez será más rápido. la mitad de la longitud del lado del cuadrado ya la hemos determinado para el caso anterior, con lo cual bastará con tomarla con el compás y llevarla sobre el lado: [14]. para situar el centro de la circunferencia del pétalo a la misma distancia del vértice del cuadrado que antes, haremos lo siguiente: tomamos con el compás el radio del pétalo que hemos trazado anteriormente, desde el punto medio del lado del cuadrado trazamos un arco, y donde corte a la diagonal, ahí está el centro: [15]. conociendo el centro y el radio, ya sólo falta trazar la circunferencia: [16]
para los dos pétalos de la parte inferior, se repetirían los mismos pasos. como observación final, si los pétalos tuvieran como radio la mitad del lado del cuadrado pequeño, se tocarían entre sí, y como decía más arriba, eso no sucede.
pues hala, ya está. os gusta cómo ha quedado? :D me sentiré satisfecho si a partir de ahora veis con otros ojos los pétalos, digo las baldosas. :P
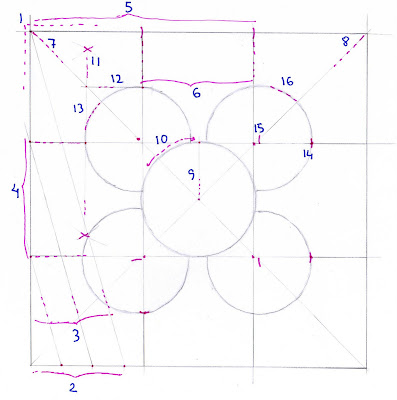
sabía que antes o después escribiría alguna entrada sobre baldosas, pero hay muchas que tienen dibujos interesantes y nunca sabía cuál elegir como ejemplo. hace poco he sabido que las baldosas de bilbao -ciudad que he visitado en numerosas ocasiones desde mi infancia debido a los vínculos familiares que me unen a ella- son únicas y tienen mucha historia. por eso he decidido rendir un homenaje a la baldosa de bilbao. ;)
lo primero de todo es dibujar un cuadrado, de la longitud del lado que se desee, pero a ser posible amplio para poder hacer construcciones sobre él cómodamente: [1]. en aquella entrada que escribí sobre los polígonos, tenéis explicado cómo dibujar un cuadrado. ;)
a continuación vamos a dividir sus lados en tres partes iguales en horizontal y en vertical, para obtener 3x3 cuadrados cuyo lado sería un tercio del lado del original.
empezaremos dividiendo el lado vertical izquierdo en tres partes iguales. para ello utilizaremos el teorema de thales. nos serviremos de las propias líneas del cuadrado, con objeto de no trazar líneas adicionales que compliquen más el dibujo. sobre el lado horizontal inferior del cuadrado, llevamos una misma distancia, elegida a voluntad, tres veces: [2]. trazamos una línea que una el extremo más ‘lejano’, donde hemos llevado esa distancia por tercera vez, con el vértice superior izquierdo del cuadrado; desde el punto del lado horizontal donde nos hemos llevado la distancia arbitraria por segunda vez, trazamos una paralela a la última línea citada; y desde el punto donde nos hemos llevado por primera vez la distancia ‘de thales’, trazamos otra paralela a esa línea; de ese modo, hemos dividido el lado vertical izquierdo en tres partes iguales: [3].
desde los puntos que marcan la división de ese lado, trazamos sendas líneas paralelas al lado horizontal del cuadrado: [4]. de ese modo, hemos dividido el cuadrado en tres ‘rebanadas’ o capas horizontales del mismo espesor.
a continuación haremos algo análogo desde el lado horizontal, y por seguir un orden, lo haremos en el superior. para dividirlo en tres partes iguales no será necesario aplicar el teorema de thales nuevamente. como ya tenemos dividido el lado vertical, tomamos con el compás la longitud de ‘un tercio de lado’, y desde el vértice del cuadrado la llevamos dos veces sucesivamente: [5]. desde esos puntos que dividen el lado horizontal en tres partes iguales, trazamos dos paralelas al lado vertical del cuadrado: [6]. como ya estaba cortado en tres ‘rebanadas’ horizontales, al darle esos nuevos cortes verticales, lo hemos convertido en 9 cuadrados de 1/3 de lado del original, en disposición 3x3.
ahora viene la parte quizá más delicada. antes que nada, vamos a trazar las dos diagonales del cuadrado grande, el original, pues nos van a hacer falta: [7] y [8]. las hacemos en trazo fino para no perjudicar mucho la estética del dibujo.
con centro en el punto de corte de las dos diagonales, que es el centro del cuadrado grande, trazaremos una circunferencia cuyo radio será la mitad del lado del cuadrado pequeño. será una circunferencia inscrita en dicho cuadrado. para ello, desde el punto de corte de las diagonales trazaremos una paralela al lado vertical del cuadrado. donde corte al lado horizontal del cuadrado pequeño, será por donde deba pasar: [9]. así pues, trazamos la circunferencia, que deberá ser tangente a los lados del cuadrado: [10]. la construcción nunca será exacta, y para que se parezca a como son estas baldosas en la realidad, es mejor que la circunferencia se pase un poco de grande, que se salga ligeramente de los límites del cuadrado.
lo que viene ahora es más fácil de entender intuitivamente que de explicar. el dibujo de la baldosa de bilbao es similar a una flor con cuatro pétalos. y aunque estos pétalos están próximos, no llegan a tocarse entre sí. los cuatro pétalos son arcos de circunferencia que pasan por los puntos medios de los lados de los cuatro cuadrados pequeños que se encuentran en las esquinas del cuadrado grande. esto podría hacer pensar que su radio es igual a la mitad del lado del cuadrado pequeño, al igual que la circunferencia central. pero no es así, en realidad es un poco más pequeño. en consecuencia, el centro de la circunferencia del ‘pétalo’ no está exactamente en el vértice del cuadrado pequeño, sino ligeramente más adentro, aunque eso sí, en su diagonal.
dado que no he logrado encontrar las medidas o proporciones exactas de las baldosas de bilbao, lo haremos de forma aproximada. aunque, eso sí, siendo coherentes y manteniendo las medidas que hayamos elegido en un principio. nos situamos en el cuadrado pequeño de la esquina superior izquierda. trazamos la mediatriz del lado inferior de este cuadrado para hallar su punto medio: [11]. en la entrada de los polígonos también explicaba cómo trazar una mediatriz, lo digo por no alargar más esto, que parece la biblia. :D bien, nos fijamos en dónde la mediatriz ha cortado a la diagonal, y desde ese punto de corte trazamos una paralela al lado horizontal del cuadrado. de ese modo dividimos también en dos el lado vertical del cuadrado sin tener que trazar una nueva mediatriz: [12].
elegimos un punto próximo al vértice del cuadrado pequeño, que se encuentre en el interior del mismo y en su diagonal. desde ese punto comenzamos a trazar una circunferencia que pase por los puntos medios de los lados del cuadrado que acabamos de determinar, y detenemos su trazado cuando corte a la circunferencia central: [13].
a continuación haremos lo mismo en el cuadrado pequeño superior derecho, pero esta vez será más rápido. la mitad de la longitud del lado del cuadrado ya la hemos determinado para el caso anterior, con lo cual bastará con tomarla con el compás y llevarla sobre el lado: [14]. para situar el centro de la circunferencia del pétalo a la misma distancia del vértice del cuadrado que antes, haremos lo siguiente: tomamos con el compás el radio del pétalo que hemos trazado anteriormente, desde el punto medio del lado del cuadrado trazamos un arco, y donde corte a la diagonal, ahí está el centro: [15]. conociendo el centro y el radio, ya sólo falta trazar la circunferencia: [16]
para los dos pétalos de la parte inferior, se repetirían los mismos pasos. como observación final, si los pétalos tuvieran como radio la mitad del lado del cuadrado pequeño, se tocarían entre sí, y como decía más arriba, eso no sucede.
pues hala, ya está. os gusta cómo ha quedado? :D me sentiré satisfecho si a partir de ahora veis con otros ojos los pétalos, digo las baldosas. :P

Comentarios
Publicar un comentario