nieve
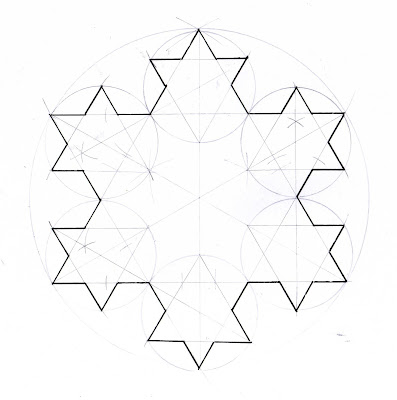
esta figura es la representación simplificada de la forma que adopta un copo de nieve.
la manera de generarla es sencilla. se parte de un triángulo equilátero. se divide cada uno de sus lados en tres partes iguales, y desde cada uno de los tramos medios resultantes de esta división se construye un nuevo triángulo equilátero.


hemos obtenido algo similar a una estrella de david. sobre cada una de las líneas rectas de la estrella podemos repetir el proceso: las dividimos en tres partes iguales, y sobre cada tramo medio trazamos nuevos triángulos equiláteros.

y así se podría seguir indefinidamente. no continuamos el proceso, porque el número de nuevos triángulos generados va aumentando exponencialmente, y su tamaño cada vez más pequeño hace difícil dibujarlos.
se puede obtener una ley recurrente para calcular el perímetro y el área de la figura tipo ‘copo de nieve’ que se obtiene al realizar sucesivamente el proceso de construir triángulos sobre los tramos medios de sus lados.

el perímetro del triángulo equilátero del que se parte es igual a 3 veces la longitud de su lado. y su área será, como para todo triángulo, la mitad del producto de su base por su altura. la altura de un triángulo equilátero es su lado multiplicado por √3/2.

en la primera fase del proceso, cada tramo medio del triángulo equilátero lo hemos sustituido por los dos lados de un nuevo triángulo cuya longitud es 1/3 del lado inicial. es decir, 2/3 del perímetro inicial lo hemos dejado como estaba, y 1/3 del mismo lo hemos duplicado. esto da como resultado multiplicar el perímetro inicial por 4/3 (ver los cálculos en el escaneado).
el perímetro así obtenido será igual a 4 veces el lado inicial, o bien igual a 12 veces por 1/3 de este lado. la ‘estrella de david’ tiene 12 lados o líneas rectas.
así sucederá en todas las fases del proceso. siempre multiplicaremos el perímetro que teníamos en la fase anterior por 4/3. y los lados de las figuras obtenidas, puesto que vamos dividiendo su longitud entre 3 cada vez, irán divididos entre las potencias de 3: 1/3, 1/9, 1/27, 1/81...
en cuanto al área, será igual a la del triángulo inicial más la de los 3 triángulos que hemos generado. dado que el área de un triángulo depende del cuadrado de su lado, si el lado del nuevo triángulo es 1/3 del lado del triángulo inicial, su área será (1/3)*(1/3)=1/9 del área del triángulo inicial.

en la segunda fase, el perímetro pasará a ser el de la primera multiplicado por 4/3, lo que da como resultado 16/3 del lado del triángulo inicial, o bien 48 por 1/9 de dicho lado, que es la longitud de los lados de los triángulos que hemos generado esta vez.
el área será igual a la obtenida en la primera fase más la de los 12 nuevos triángulos -tantos como líneas rectas tenía la estrella de david de la fase anterior-, cuyo lado es 1/9 del lado inicial. su área será (1/9)*(1/9)=1/81 del área del triángulo inicial.

vamos a aplicar el proceso de generar nuevos triángulos una vez más. no he dibujado la figura resultante, pero nos la podemos imaginar.
el nuevo perímetro será igual a 4/3 por el perímetro obtenido en la segunda fase, y eso es igual a 64/9 por el lado del triángulo inicial. o bien, 192 veces por el lado de los nuevos triángulos generados, cuya longitud será 1/27 del lado inicial.
la figura obtenida en la segunda fase tenía 48 líneas rectas, y por tanto se habrán generado 48 nuevos triángulos. el área de cada uno de ellos será (1/27)*(1/27)=1/729 del área del triángulo inicial.

veamos la expresión general del perímetro y el área de la figura obtenida cuando realizamos este proceso un número genérico n de veces.
el perímetro final será igual a 4/3 elevado a n por el perímetro inicial. dado que 4/3 es un número mayor que 1, cuando n tiende a infinito el perímetro se hace infinito también.
el área final será igual a la suma de las áreas obtenidas en cada fase. observamos que a partir de la primera fase se sigue una progresión geométrica de razón 4/9. para hallar su valor cuando n tiende a infinito, emplearemos esta conocida fórmula: la suma de los términos de una progresión geométrica de razón r<1 es igual a 1/(1-r).
así pues, al aplicar el proceso de generar triángulos en los tramos medios infinitas veces, la figura obtenida tendrá un área igual a 8/5 (es decir, 1.6) por la del triángulo inicial.
ahí está la gran paradoja de la figura del copo de nieve: su perímetro puede crecer hasta el infinito, mientras que su área siempre es finita.
Comentarios
Publicar un comentario