el cono

parece que en los planes de estudios de primaria y e.s.o. se da mucha importancia al estudio del cono. yo pensaba que el cono era una figura geométrica sin mayor importancia que cualquier otra, pero en fin... me tendré que poner al día, por si se lo tengo que explicar a mi alumna.

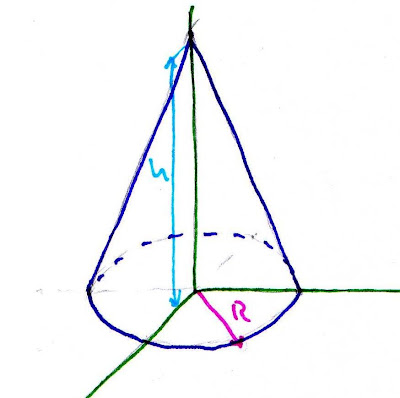
veamos, un cono se puede definir de manera sencilla como la figura geométrica que se obtiene al hacer girar un triángulo rectángulo sobre uno de sus catetos.

al cortar el cono por un plano que contenga al eje de revolución, la sección será el triángulo isósceles resultante de juntar el triángulo rectángulo que lo ha generado y su simétrico. y al cortarlo por un plano perpendicular al eje de revolución, se obtendrá una sección circular.

llamaremos R al radio de la base del cono, y h a su altura. R y h son los catetos del triángulo rectángulo generador del cono.

a ver, qué cosas nos pueden pedir sobre un cono? ya sé, su volumen. creo recordar que era igual al producto de su base circular por su altura, y todo eso partido por 3. es decir, π·R²·h/3.

vamos a asegurarnos. lo haremos integrando en coordenadas cilíndricas. integraremos ‘discos’ de un radio genérico ρ y de espesor infinitesimal dz.

tenemos que encontrar una relación entre el radio ρ de cada sección del cono y su coordenada vertical z. sabemos que esta relación es de carácter lineal y conocemos el valor del radio en la base y en el vértice del cono. para z=0, ρ=R (base); y para z=h, ρ=0 (vértice).

así pues, la expresión de ρ en función de z será: ρ=R-(R/h)·z

el volumen del cono será, como decíamos, la integral de los volúmenes de los discos de radio ρ y espesor dz. nuestra variable de integración será la coordenada vertical z, y variará entre la base del cono (z=0) y su vértice (z=h).

el volumen de cada uno de los discos será el producto de su área circular (π·ρ²) por su altura (dz). π se puede sacar de la integral al ser una constante. por otro lado, ρlo sustituimos por la expresión que hemos obtenido más arriba, de tal modo que podamos integrar en z.

desarrollamos aparte la expresión [R-(R/h)·z]²para poder integrar con más comodidad.

y por fin, integramos. se trata de una integral polinómica cuyo límite inferior (z=0) es nulo, por lo que directamente ponemos su valor en el límite superior (z=h).

que no se nos olvide que habíamos sacado π fuera de la integral. el resultado que hemos obtenido tenemos que multiplicarlo por π. así pues, el volumen del cono será:

curiosamente este valor es un tercio del volumen de un cilindro de radio R y altura h. es fácil comprender que el volumen de un cono es menor que el de un cilindro que tenga la misma base y la misma altura, pero sólo calculandolo hemos podido averiguar cuál es la proporción exacta.

es decir, si imaginamos un cilindro de radio R y altura h y un cono inscrito dentro del mismo con la misma base y altura, el volumen del cono será 1/3 del total, mientras que el volumen de la parte restante, “lo que no es cono”, será 2/3 del total. el volumen del cono es la mitad del volumen del “negativo del cono”. la proporción es 1:2.

disculpadme un momento, que me están diciendo algo por aquí...

me dicen que eso que llaman ‘cono’ que estudian los niños no es el cono como figura geométrica, sino que es una asignatura llamada ‘conocimiento del medio’.

después de todos los cálculos que he hecho... ya me parecía a mí raro. :P

--------------------------------------------------------------------------------------------

dejamos por ahora los cálculos matemáticos y los chistes nefastos. :D pasamos a otro asunto: mi amiga anele me ha propuesto un bonito reto que consiste en poner una frase que haya leído últimamente y que me haya llamado la atención. esta propuesta no podía llegar en mejor momento.

la frase es de un personaje ilustre como fue el doctor sigmund freud. más que una frase es un párrafo. creo que no necesita ninguna explicación...

“nunca estamos tan indefensos contra el sufrimiento como cuando amamos; nunca nos sentimos tan desconsoladamente desgraciados como cuando hemos perdido nuestro objeto amado o su amor”.

ahora les paso el testigo a rosana, a wendy y a gen. las tres leéis mucho y sois muy reflexivas, cada una a vuestra manera, y por eso creo que este reto os gustará. :)