número de euler

tenía pendiente hablar del número e, también llamado número de euler. es tan importante en las matemáticas -y en definitiva en la naturaleza- como π o como el número áureo.

para ello hay que recordar el concepto de derivada. la derivada de una función es otra función que viene a representar su variación en cada punto, su pendiente.

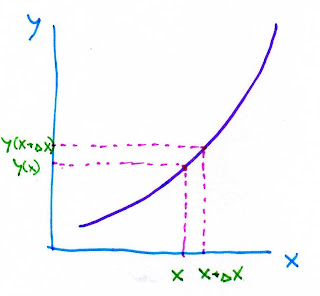
el crecimiento de una función entre dos puntos viene representado por el cociente entre la diferencia de ordenadas y la diferencia de abscisas. si la diferencia de abscisas la reducimos a un valor infinitesimal Δx, la derivada será por definición el límite cuando Δx tiende a 0 de la diferencia entre los valores que toma la función en x y en x+Δx dividida entre la longitud del intervalo, Δx.

existe alguna función para la cual su derivada sea igual en todos los puntos a la propia función? la respuesta es afirmativa. y sabemos que esa función va a ser una exponencial del tipo k^x, siendo k un número constante y x la variable.

cuando aplicamos la definición de derivada a una función de este tipo, y sabiendo que el producto de potencias de la misma base es igual a la suma de exponentes, obtenemos que la derivada es igual a un cierto límite cuando Δx tiende a 0 -que será una constante-, multiplicado por la función inicial k^x.

la derivada de una función exponencial, por tanto, es igual a una constante multiplicada por esa función exponencial. la constante es un límite que depende de k, la base de la exponencial. podemos suponer que existirá un valor de la base para el cual el valor de la constante C será 1, y por tanto la derivada de la función será igual a la propia función.

llamaremos a esa función que buscamos e^x. e es un número que sabemos que existe, pero aún no conocemos su valor.

toda función puede aproximarse mediante una serie polinómica infinita del tipo a₀+a₁·x+a₂·x²+a₃·x³+... los coeficientes a_n, o bien tendrán signos alternados -unos suman y otros restan-, o bien, en caso de que sean todos del mismo signo, tendrán valores decrecientes según avanza el grado del polinomio. de otro modo, se nos dispararía hasta el infinito.

tomamos un polinomio de esa forma y lo derivamos. recordemos que la derivada de una función monómica del tipo xⁿ es igual a la base elevada al exponente menos una unidad, multiplicada por el exponente.

a continuación, obligamos a que la derivada de nuestro polinomio sea igual al propio polinomio inicial. para cada grado de la variable x, el coeficiente del primer polinomio debe ser igual al del segundo polinomio. observar en el escaneado anterior las flechas que indican cómo deben corresponderse los coeficientes.

llegados a este punto, hay que recordar el concepto de factorial. el factorial de un número entero es igual al producto de dicho número por todos los anteriores hasta llegar al 1 (o al 2, según cómo se mire, porque multiplicar por 1 no tiene ningún efecto). el factorial de un número n se representa por n seguido de un signo de exclamación, n! (no sé a quién se le ocurrió eso), y será igual a n·(n-1)·(n-2)·...·3·2·1.

hemos llegado a la conclusión de que cada coeficiente de nuestro polinomio se puede expresar en función del término independiente, el coeficiente de grado 0. el coeficiente de grado genérico n, a_n,será igual a a₀ dividido entre el factorial de n.

pero, cuánto vale a₀? a₀ será el valor del polinomio en x=0. excepto el término independiente, todos los demás se anularán. recordemos que la función que estamos aproximando mediante el polinomio es una exponencial: e^x. valga lo que valga e, la exponencial en x=0 será igual a 1, pues cualquier número distinto de cero elevado a 0 es igual a la unidad. por tanto, a₀ será igual a 1.

así pues, podemos decir que el coeficiente de grado n de nuestro polinomio será igual a 1 dividido entre el factorial de n.

y ahora llegamos al momento de la verdad: cuánto vale el número e? e es la base de la exponencial, por lo que tendrá el valor que ésta tome en x=1. para calcular ese valor, sustituiremos en nuestro polinomio x por 1.

por tanto, e será igual al valor que toma en el límite la suma de la serie 1+(1/1!)+(1/2!)+(1/3!)+... el número e, con una aproximación suficiente, será igual a 2.718281828459...

hoy me he levantado con ganas de números, porque con los números me siento como pez en el agua. no en vano los reyes me han traído un libro de historia de las matemáticas. además, un pack de los programas de gaby, fofó y miliki para recordar la infancia -este regalo es para todos los de casa, realmente-, y una caja recopilatoria de christina rosenvinge.

el otro día me hice esta autofoto en la que, según me dijeron, tenía cara de bueno. va a ser por eso que los reyes se han portado bien. :)