otra de pitágoras

hay una manera de demostrar el teorema de pitágoras, más intuitiva y visual que la que expliqué en esta otra entrada. la otra vez nos basábamos en la semejanza de triángulos, y esta vez nos vamos a basar en las áreas.

vamos a seguir los siguientes pasos:

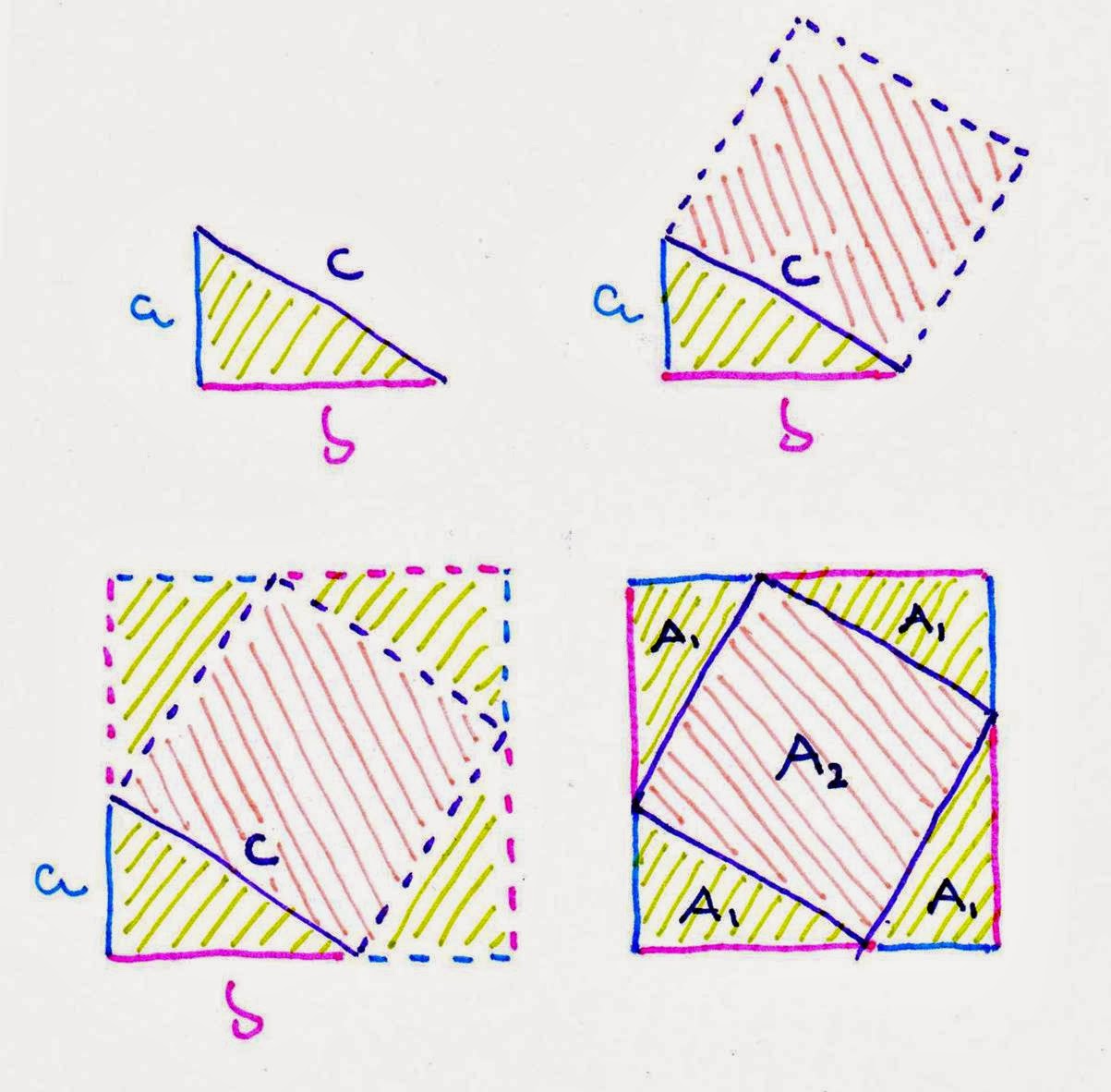
• partimos de un triángulo rectángulo cualquiera, de catetos a,b y de hipotenusa c.
• trazamos un cuadrado cuyo lado sea la hipotenusa.
• nos damos cuenta de que podemos encajar tres triángulos más idénticos al original, formando un cuadrado más grande cuyo lado es la suma de los dos catetos, a+b, y que contiene en su interior al cuadrado cuyo lado era la hipotenusa, c.
• llamamos A₁ al área de cada uno de los triángulos rectángulos -rayada en color verde pistacho-, y A₂ al área del cuadrado interior -rayada en color rosa salmón-.

por una parte, sabemos que el área total será la del cuadrado de lado a+b. y por otra parte, esa área total será igual a la suma de las áreas de los cuatro triángulos rectángulos más la del cuadrado de lado c.

sabiendo que el área de un triángulo es igual a la mitad de la base por la altura, y conociendo la fórmula que nos da el cuadrado de una suma, desarrollamos ambas expresiones y las igualamos. operamos, y nuestra conclusión no es otra que el teorema de pitágoras: la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.