mi mundo de papel

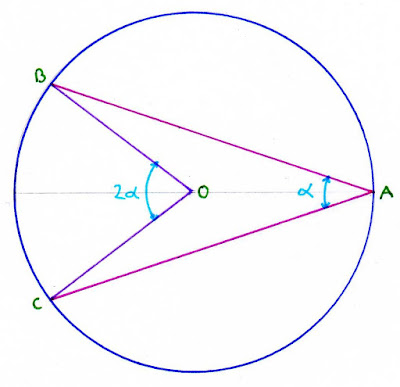
en dibujo técnico de cou, aprendimos una interesante propiedad. desde un punto A de una circunferencia, se trazan dos líneas que forman entre sí un ángulo α . dichas líneas cortan a la circunferencia en los puntos B y C. pues bien, los radios OB y OC formarán un ángulo 2· α , el doble del que formaban las líneas AB y AC que habíamos trazado al principio. esta propiedad se demuestra de la siguiente manera. los triángulos OAB y OAC -aparte de ser iguales entre sí- son isósceles, ya que dos de sus lados son radios de la circunferencia. tendrán dos ángulos agudos iguales a α /2. sabiendo que los tres ángulos de cualquier triángulo suman 180º, se puede deducir que el ángulo desigual medirá 180– α . el ángulo formado por OB y la prolongación de OA será el suplementario del ángulo obtuso que acabamos de calcular. y si éste era igual a 180– α , el suplementario será α . y finalmente, el ángulo que forman OB y OC será el doble, es decir 2· α , como queríamos demostrar. nunca se me olvidará que,

siempre digo que la ropa de verano me gusta más que la de invierno. para el frío tengo lo justo y necesario, me da mucha pereza comprarme ropa nueva. en cambio, en verano siempre estreno alguna prenda un poco atrevida. ya hablé hace tiempo de lo bien que combinan los colores rosa y gris . en cierto modo, el gris representa la parte más racional y matemática de la vida, mientras que el rosa corresponde a la faceta más emocional y romántica. y por eso este año he decidido casi sin pensarlo combinar esos dos colores, con una camiseta rosa y unas bermudas de algodón grises. llevaré este conjunto a las quedadas y otras ocasiones especiales. ;) me faltan unas chanclas para completar el conjunto. he encontrado unas baratas y que tienen las correas de tela como a mí me gusta -las de plástico se me clavan-. no están mal, pero no descarto encontrar otras más bonitas.

no puedo negarlo, me gustan los números complejos más que a un tonto un lápiz. y en particular esta fórmula, que me ha dado juego para varias entradas. e ix = cos(x) + i·sen(x) dicha fórmula relaciona las funciones exponenciales con las funciones senoidales a través de los números complejos, y gracias a ella las exponenciales y las senoidales pueden transformarse unas en otras, en ambos sentidos. algo así como cuando mortadelo se disfraza... a partir de la mencionada ecuación, vamos a despejar el seno y el coseno , para hallar después la tangente como razón entre ambos. haremos algo parecido a un sistema de ecuaciones, teniendo en cuenta que el seno es una función impar y el coseno es una función par. ahora vamos a obtener la función inversa de la tangente, es decir la arcotangente . para ello, en primer lugar intercambiamos las variables x, y . a continuación despejamos y , tomando logaritmos. la derivada de la función arcotangente es 1/(1+x 2 ) . por definición, arcotg(x) es e